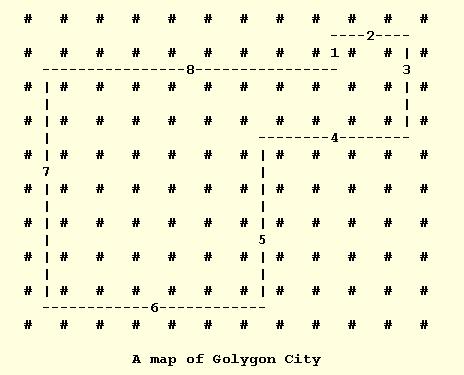
Golygon City

Auch eine Reise über tausend Kilometer muss mit einem einzelnen Schritt beginnen (Laotse)

Lassen Sie sich auf einen Spaziergang durch Golygon City oder eine andere Stadt mit einer schachbrettartigen Straßenanordnung wie New York, Tokio oder Mannheim ein.
Sie müssen sich nur an ein einfaches Schema halten:
Gehen Sie zunächst um einen Häuserblock in beliebiger Richtung und wenden sich danach nach rechts oder links. Gehen Sie nun zwei Blocks geradeaus und biegen dann wieder nach rechts oder links ab. Danach gehen Sie drei Blocks geradeaus und so weiter. Nach jedem Abbiegen gehen Sie einen Block weiter geradeaus als zuvor. Wenn Sie nach einiger Zeit wieder genau am Ausgangspunkt landen, haben Sie ein Golygon abgeschritten.

Eigenschaften von Golygonen

Ein Golygon besteht aus einer endlichen Anzahl von Geradenstücken, der Längen eins, zwei, drei, usw. Jedes Stück schließt
rechtwinklig an das vorübergehende an und ist genau eine Einheit länger. Wenn das erste Stück rechtwinklig mit dem längsten verbunden ist,
welches am Ausgangspunkt endet, dann entsteht ein Golygon.

Golygone wurden in den 80 er Jahren von Lee Sallows erfunden, einem Ingenieur an der Katholischen Universität Nijmegen. Sein erstes Golygon war das oben abgebildete acht-seitige Golygon. Es gelang ihm nicht, ein Golygon mit weniger Seiten zu finden. Auch bei der Suche nach Golygonen mit mehr als acht Seiten stieß er zunächst auf Schwierigkeiten.

Aufgaben

1. Zeichnen Sie das oben abgebildete Golygon auf kariertem Papier nach.
2. Versuchen Sie, weitere Golygone mit acht Seiten zu finden.
3. Kann es Golygone mit weniger als acht Seiten geben? Versuchen Sie die Antwort zu begründen.
4. Warum kann es kein Golygon mit vier Seiten geben?
5. Versuchen Sie, ein Golygon mit mehr als acht Seiten zu finden.

Die Idee zu dieser Aufgabe enstammt der Zeitschrift ‚Spektrum der Wissenschaft' - Dossier 02/03: Mathematische Unterhaltungen, S. 25.

In der Tat gibt es nur ein einziges Golygon mit acht Seiten. Auf der Suche nach Golygonen mit mehr als acht Seiten kann man mathematisch begründen, dass die Seitenzahl eines Golygons immer ein Vielfaches von acht sein muss. D.h. es gibt Golygone mit 8, 16, 24 Seiten usw.
Die Suche nach Golygonen mit 16 Seiten allerdings ist schon sehr mühsam, da es insgesamt 2^16 = 65536 Möglichkeiten für rechtwinklige Geradenanordnungen gibt, davon aber nur 24 richtige Golygone sind.